In a parallel group-randomized trial (GRT), also called a parallel cluster-randomized trial, groups or clusters are randomized to study conditions, and observations are taken on the members of those groups with no cross-over of groups or clusters to a different condition or study arm during the trial (; ; ; ; ). This design is common in public health, where the units of assignment may be schools, worksites, clinics, or whole communities, and the units of observation are the students, employees, patients, or residents within those groups. It is common in animal research, where the units of assignment may be litters of mice or rats and the units of observation are individual animals. It is also common in clinical research, where the units of assignment may be patients and the units of observation are individual teeth or eyes. Special methods are needed for analysis and sample size estimation for these studies, as detailed below and in the parallel GRT sample size calculator.
Features and Uses
Public Health and Medicine
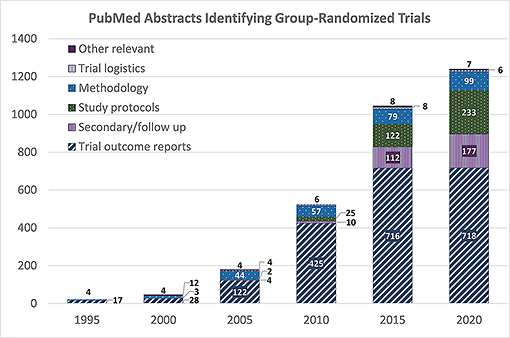
The GRT design is increasingly common in public health and medicine, and the literature on the design, analysis, and use of GRTs has grown rapidly over the last 25 years. The accompanying figure demonstrates this growth, showing that the number of PubMed abstracts that identify GRTs for human studies more than doubled every 5 years from 1995 through 2015, with continued but less dramatic growth through 2020.
Animal Research
Parallel GRTs are common in animal research, where the units of assignment may be litters of mice or rats, or other collections of animals. The design and analytic issues are the same, whether the study involves human or animals, and whether the research is applied or basic.
Tabular data and full-size version
Webinars and Training
- Methods: Mind the Gap Webinar – Choosing Sample Sizes for Multilevel and Longitudinal Studies Analyzed with Linear Mixed Models
- NIH Pragmatic Trials Collaboratory Grand Rounds: Methods for Handling Missing Data in Cluster Randomized Trials
- Pragmatic and Group-Randomized Trials in Public Health and Medicine Course
Nested or Hierarchical Design
Parallel GRTs have a nested or hierarchical design: the groups randomized to each study condition are nested within those study conditions so that each group appears in only one study condition.
The members are nested within those groups so that each member appears in only one group. In cohort GRTs, members are observed repeatedly so that measurements are nested within members; in cross-sectional GRTs, different members are observed in each group at each measurement occasion. In each case, the units of observation are nested within the units of assignment, which are nested within the study conditions.
Appropriate Use
Parallel GRTs can be employed in a wide variety of settings and populations to address a wide variety of research questions. They are the best comparative design available when the investigator wants to evaluate an intervention that:
- operates at a group level,
- manipulates the social or physical environment, or
- cannot be delivered to individual participants without substantial risk of contamination.
Potential for Confounding
Parallel GRTs often involve a limited number of groups randomized to each study condition. A recent review found that the median number of groups randomized to each study condition in GRTs related to cancer was 25, though many were much smaller (). When the number of groups available for randomization is limited, there is a greater risk that potentially confounding variables will be unevenly distributed among the study conditions, and this can threaten the internal validity of the trial. As a result, when the number of groups to be randomized to each study condition is limited, a priori matching and a priori stratification are widely recommended to help ensure balance across the study conditions on potential confounders (; ; ;
) More recently, constrained randomization is recommended as another option for parallel GRTs (; ).
Intraclass Correlation
The more challenging feature of parallel GRTs is that members of the same group usually share some physical, geographic, social, or other connection. Those connections create the expectation for a positive intraclass correlation (ICC) among observations taken on members of the same group, as members of the same group tend to be more like one another than to members of other groups. The ICC is simply the average bivariate correlation on the outcome among members of the same group or cluster.
Positive ICC reduces the variation among the members of the same group but increases the variation among the groups. As such, the variance of any group-level statistic will be larger in a parallel GRT than in a randomized clinical trial (RCT). Complicating matters further, the degrees of freedom (df) available to estimate the ICC or the group-level component of variance will be based on the number of groups, and so are often limited. Any analysis that ignores the extra variation (or positive ICC) or the limited df will have a type I error rate that is inflated, often badly (; ; ; ; ).
Solutions
The recommended solution to these challenges is to employ a priori matching, a priori stratification, or constrained randomization to balance potential confounders, to reflect the hierarchical structure of the design in the analytic plan; and to estimate the sample size for the GRT based on realistic and data-based estimates of the ICC and the other parameters indicated by the analytic plan. Extra variation and limited df always reduce power, so it is essential to consider these factors while the study is being planned, and particularly as part of the estimation of sample size.
The sections below provide additional resources for investigators considering a parallel group- or cluster-randomized trial.